Text Classification using Naive Bayes Classifier
- hxr8557
- Nov 14, 2022
- 6 min read
Naive Bayes algorithm is commonly used for text classification. In this blog, we will deep dive through NBC concepts and its implementation.
A Naive Bayes classifier is a probabilistic machine learning model that’s used for classification task. The crux of the classifier is based on the Bayes theorem. [1]
The Bayesian approach considers both prior belief and Evidence. Where as, in Frequentist method, it only considers the evidence. The frequentist approach assigns probabilities to data, not to hypotheses, whereas the Bayesian approach assigns probabilities to hypotheses. [2]
Naive Assumption:
The word "Naive" in the NBC, comes from the fact that - it makes a naive assumption of conditional independence of the events. For example, if A and B are two independent events, they will not have any link with each other. This Naive assumption plays a very important role in NBC.
Bayes' Theorem:
The Bayes' theorem computes the conditional probability using the joint probability between the features and possible labels with the marginal probability of the features occurring across all possible labels. Naive Bayes, makes use of the Bayes theorem to compute the conditional probability. [3]
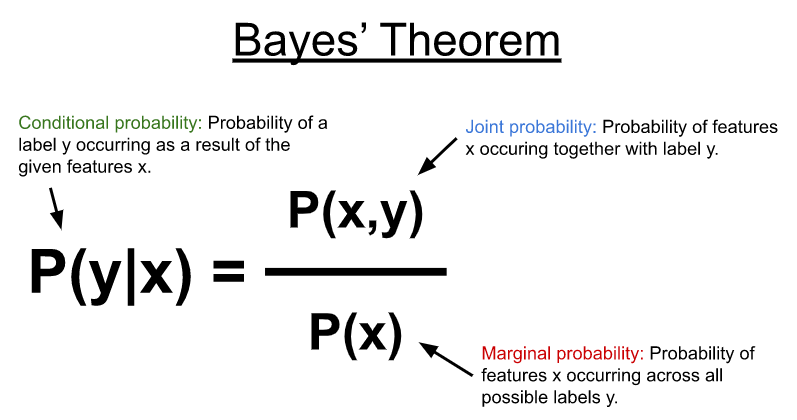
Image source : https://developer.nvidia.com/blog/faster-text-classification-with-naive-bayes-and-gpus/

Image : Handwritten formula - as taught in the class
Applications of NBC :
Social Media text classification - sentiment analysis
Spam mail detector
It is widely used for multi-class predictions.
Now, let's go through the implementation of the Naive Bayes Classifier.
1 - Import statements:
Below are the imports that I've used, in my code. Along with numpy, pandas, I'm also using gensim and nltk.
gensim and re - For the effective pre-processing of the text
nltk - To fetch the stop words in English (most commonly used words in English)
2 - Reading the data file
Note : In this assignment, I'm considering only 8000 rows in the dataframe out of the entire data, as my notebook crashed for very huge data. So, here we will be dealing with data with 8k rows

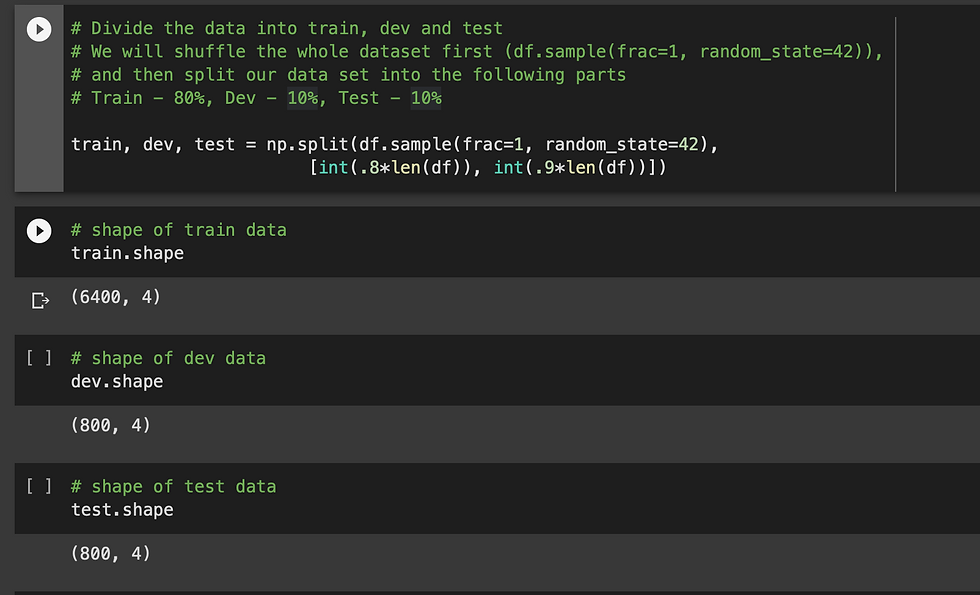
3 - Dividing the data into 3 parts - train, dev and test
train - 80 %
dev - 10 %
test - 10 %
4 - Displaying the train data

5 - Defining the functions to preprocess the train data
I've written two functions with slight variations to pre-process the train_data.
The first function, preprocess - is used to preprocess each row in the data individually and returns a list of words w.r.t each row
I'm using regular expressions - to remove special characters, digits, extra spaces, leading and trailing spaces etc from the sentence.
Also, for the easy processing I'm using genesis.utils.simple_preprocess to convert the sentence into a list of words
And, as a last step, I'm excluding all the stopwords in the list of words of that respective sentence

6 - Building Vocabulary dictionary
In this step, I am building the vocabulary for the training data ( {word : occurence} )
In this vocab, the words whose occurrence is less than 5, will be omitted.
To omit the less occurrence words, first I'm building a separate dictionary for rare words
And the, compare the vocab with rare words - and remove all the rare_word from the vocab

Printing the initial vocabulary, rare_words, and then - the processed vocabulary (excluding rare words)

7 - Fetching the unique class labels in the data

8 - Divide the training_data into different subsets that will contain only the unique class labels
Based on the unique class labels obtained in the above step, divide the data into subsets. Here, Since we have 6 unique class labels - I'm dividing the data into 6 different subsets for each class type respectively.
Printing a sample subset of responsibility df

Data which contains only the class type - "Experience"

9 - Creating the processed list of rows for each subset data that was created in the previous step.

Printing the processed documents in each subset data of unique class
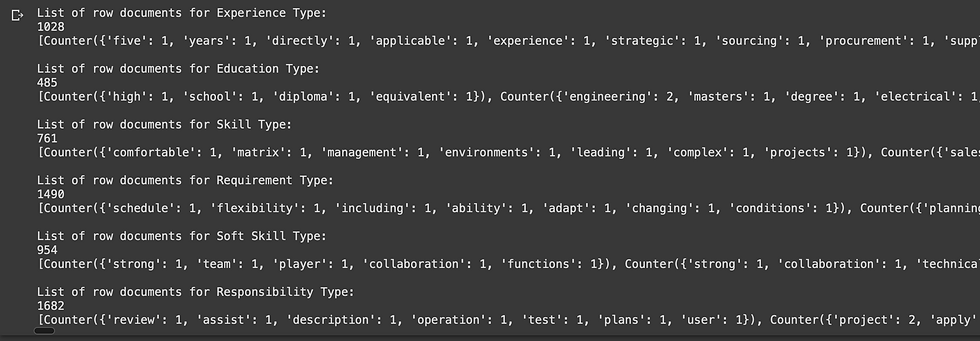
10 - Calculating the probability of occurrence of each word in present in the processed vocabulary dictionary

Displaying the calculated probability occurrence for each word

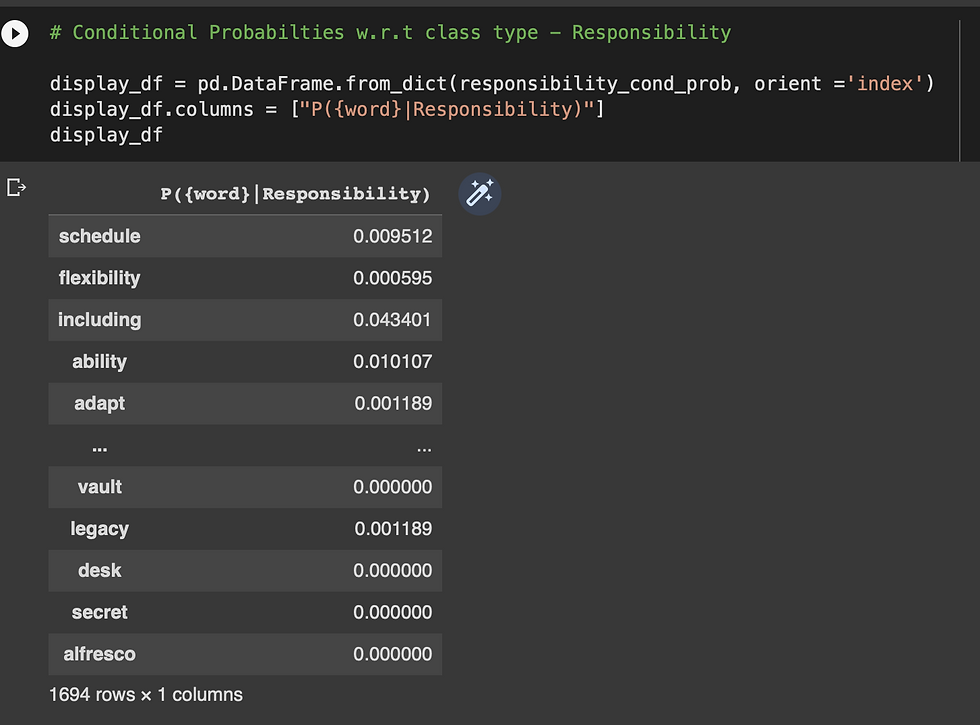
11 - Calculate the conditional probabilities for each word w.r.t to each unique class type

P( {word} | Responsibility )

P( { word} | Education )

P( { word} | Requirement )

P( { word} | Skill )

P( { word} | Soft Skill )

P( { word} | Responsibility )
12 - Defining the Naive Bayes function to compute the probability of each class.
This function will compute the probability of each class using bayes theorem
Once the probability of each class is calculated, it will be stored in a dictionary
In the end, the class type with the max probability value will be the predicted class type for the given sentence


13 - Now, use the dev data to calculate the initial accuracy

Preprocess the dev data:

14 - Defining a function to predict the class type of each sentence.
This function predicts the class type of each sentence (row) in the given dev data
For each row in the data, it applies the bayes theorem to compute the probability of each unique class
Once, the naive bayes function (defined above) returns the predicted class type, it will be appended to the list of predicted labels
I've provided the detailed comments in the code (as seen below), on how the code works

15 - Making a function call to predict the class type of each document in dev data and printing the results

16 - Defining a function to calculate the accuracy
Calculating the initial accuracy on the dev data
As seen below, the initial accuracy obtained is 59.62 %

17 - Laplace Smoothing
After obtaining the initial accuracy on dev data, in this step I implemented Laplace Smoothing to check how the accuracy would change
Before , diving into the code - let's see what is Laplace Smoothing and why do we need it? [5]
Laplace smoothing is a smoothing technique that handles the problem of zero probability in Naïve Bayes.
If the word is absent in the training dataset, then we don’t have its likelihood.
When computing probability, since we multiply all the likelihoods, the probability will become zero. This is the zero probability problem [5]

image source : [5]
Conditional probabilities for a word w.r.t to class type will be calculated using below Laplace technique: [5]
Here, alpha represents the smoothing parameter, K represents the number of dimensions (features) in the data, and N represents the number of reviews with y=positive
Defining a function to implement Laplace smoothing :
In the below code, I'm calculating the conditional probabilities using Laplace technique, mentioned above
By using the smoothing_param that is given the input, for each different values of smoothing_param the accuracy will also vary, which we will see in the later section.
I've defined another function, which will calculate the conditional probability for a missing word in training data set, by using Laplace technique
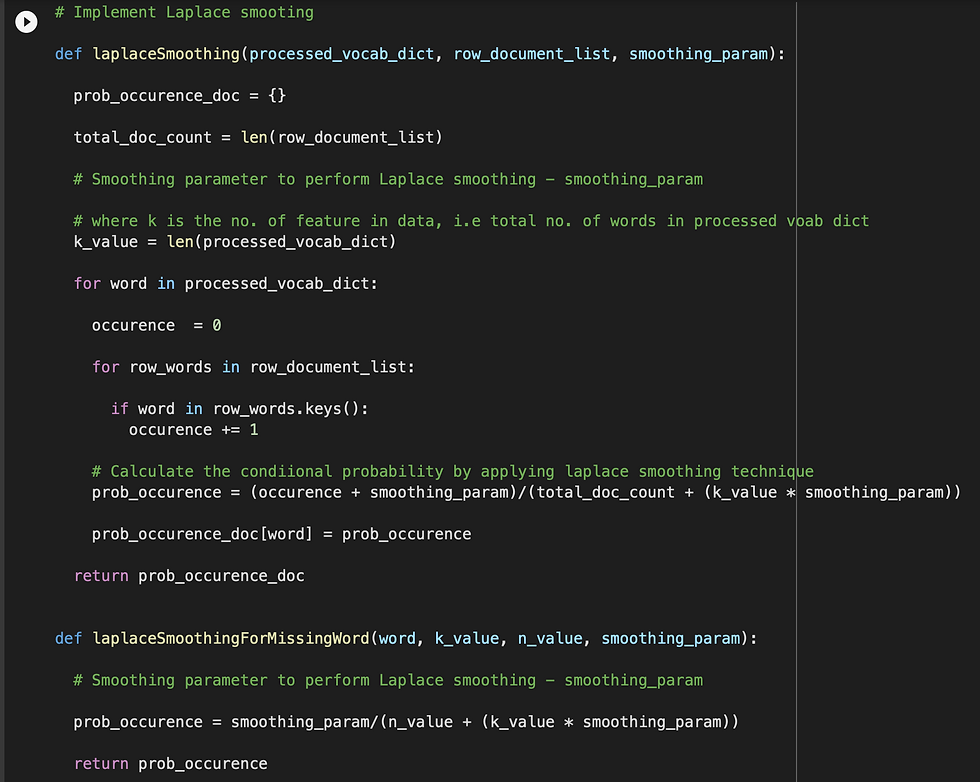
18 - Defining a function to calculate conditional probability using the given smoothing_param

19 - Displaying the conditional probability of preforming Laplace smoothing
Conditional probability of each word w.r.t to Experience class type

20 - Defining a function to predict the class type using Laplace smoothing technique
This is function is similar function, where the class type was predicted. But the difference is, it uses Laplace technique

21 - Making a function call to predict the class type use Laplace smoothing technique, and displaying the results

22 - Calculating the accuracy for dev data - using Laplace smoothing
smoothing_param = 1
Accuracy = 64.62 %
As we, observe here : the accuracy increased after applying the Laplace smoothing

23 - Experimenting with different smoothing parameters
In this step, I am finding different set of accuracies by experimenting with different smoothing parameters.
Defining a function to experiment with different values of smoothing parameters

As shown in the below screenshot, I experimented with smoothing_params = 1, 100 and 200
And, I observed that, as and when I increased the value of smoothing_param, the accuracy decreased ( as seen below)
Experiment results:
smoothing param = 1, accuracy 64.62 %
smoothing param = 100, accuracy 57.25 %
smoothing param = 200, accuracy 55.12 %
I got the highest accuracy for smoothing_param = 1

24 - Calculate the final accuracy
As the final step, calculating the final accuracy with the test data

Calculating the final accuracy with test data
As seen below, for the test data - I obtained the accuracy of 63.75%

Please refer the link below - which leads to my detailed implementation of the above mentioned code : https://github.com/harshithaharshi/datamining/blob/main/Data_Mining_Assignment2.ipynb
CONTRIBUTIONS:
Implemented the code to perform Naive Bayes classification, from the scratch
As part of the experiment, I tried experimenting with different values of smoothing parameters (as part of Laplace smoothing), to find the best smoothing parameter for test data
Below is the accuracy results for dev data, as part of my experiment:
smoothing param = 1, accuracy 64.62 %
smoothing param = 100, accuracy 57.25 %
smoothing param = 200, accuracy 55.12 %
And, as a final accuracy - I obtained 63.75% accuracy for the test data
In the process of this assignment - I was able to relate all the concepts that were taught in the class. It was a great experience to implement the Naive Bayes classifier from scratch.
CHALLENGES :
The initial struggle was to write the logic for the data-preprocessing. I explored various ways in regular expressions, gensim and stopwords removal - to be able to write a logic to process the data
The next challenge was to think over the appropriate data structures that should be used to store and retrieve the data at each stage - when a processing was done.
Planning over an appropriate data structure is very crucial for the efficiency of the code.
Implementing Laplace smoothing was a little challenging for me. As mentioned in the reference below, I read the concepts from the source mentioned to understand the logic and implement it on my own
References :
[6] - https://stackoverflow.com/questions/38250710/how-to-split-data-into-3-sets-train-validation-and-test


Comments